Trigonometry Review
After reading this page you should do Homework 1, Supplement 1.
Right Triangle Trigonometry
Recall that in a right triangle, little letters are used to indicate sides and capital letters are used for the angles, as in the diagram:
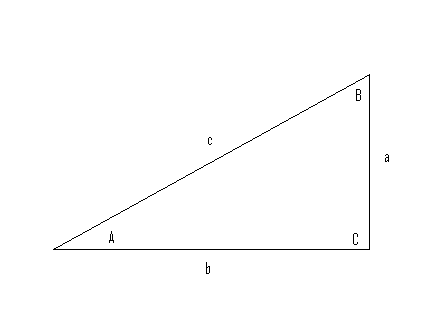
You should also remember the definitions of the 6 trigonometric functions, also called ratios, for each angle. For angle A, for instance, in this picture they are as follows:
sin(A) = a/c
cos(A) = b/c
tan(A) = a/b
csc(A) = c/a
sec(A) = c/b
cot(A) = b/a
Note that the second three trigonometric functions are the reciprocals of the first three.
The most often taught (in American high schools, in 2004) way to remember the first three ratios is: SOH CAH TOA (sin is opposite over hypotenuse, cos is adjacent over hypotenuse, and tan is opposite over adjacent). Then you just have to remember that the second three trigonometric functions are the reciprocals of the first three.
Standard position of an angle
An angle in standard position is an angle in the rectangular coordinate system with its initial side on the positive horizontal axis and rotated counterclockwise, as in the below diagram.
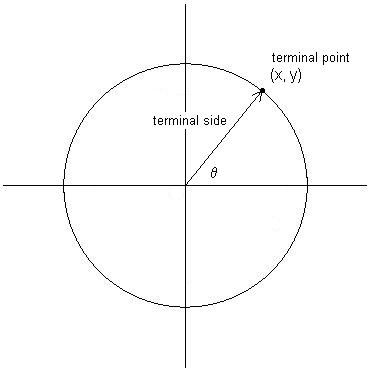
Note the meanings, indicated in diagram, of the phrases terminal side and terminal point (terminal point is not a standard term, but can be a convenient one).
Let ![]() be the length of the
terminal side. (Thus, from the Pythagorean Theorem, we have
be the length of the
terminal side. (Thus, from the Pythagorean Theorem, we have ![]() ). Then
we have the very important circle definitions of the six trigonometric
functions:
). Then
we have the very important circle definitions of the six trigonometric
functions:
![]()
![]()
![]()
![]()
![]()
![]()
Signs of the trigonometric functions in various quadrants
Note that the value of ![]() is always positive. The
value of y is positive in quadrants I and II and is negative in quadrants III
and IV. The value of x is positive in quadrants I and IV and is negative in
quadrants II and III.
is always positive. The
value of y is positive in quadrants I and II and is negative in quadrants III
and IV. The value of x is positive in quadrants I and IV and is negative in
quadrants II and III.
These facts together with the circle definitions give us rules for the signs of all six trig functions in each of the four quadrants. These rules are summarized in the following table.
|
|
Q I |
Q II |
Q III |
Q IV |
|
sin |
+ |
+ |
- |
- |
|
cos |
+ |
- |
- |
+ |
|
tan |
+ |
- |
+ |
- |
|
csc |
+ |
+ |
- |
- |
|
Sec |
+ |
- |
- |
+ |
|
Cot |
+ |
- |
+ |
- |
You probably have learned a convenient way to remember these sign rules: All Students Take Calculus. The letters A, S, T, C refer to the words “all,” “sin,” “cos,” and “tan” and tell you that all trig functions are positive in Quadrant I, sin is positive in Quadrant II (and cos and tan are negative), cos is positive in Quadrant III (and sin and tan are negative), and tan is positive in Quadrant IV (and sin and cos are negative). You have to remember also that the signs of csc, sec, and cot are the same as sin, cos, and tan, resp., because of the reciprocal identities.
Radian and degree measure
There are two common units of angle measure: degrees and radians. An angle rotated through a full circle, so that the terminal side coincides with the initial side on the positive horizontal axis, measures 360 degrees. This is equivalent to 2*pi radians (an asterisk means multiplication) and thus:
180 degrees = pi radians
This equivalence is usually used to convert between units of angle measure:
To convert from radians to degrees, multiply by 180/pi.
To convert from degrees to radians, multiply by pi/180.
Examples:
a. Convert ![]() radians to degrees.
radians to degrees.
Solution: ![]()
b. Convert 4.11 radians to degrees (round to the nearest tenth of a degree; note: a radian measure does not have to involve the number pi!).
Solution: ![]() [done in calculator, note
that your calculator has a pi key! Use it!]
[done in calculator, note
that your calculator has a pi key! Use it!]
c. Convert 75 degrees to radians. Give the exact answer, in terms of pi, and a decimal approximation to 2 decimal places (nearest hundredth).
Solution: ![]() [exact answer]
[exact answer]
In calculator: ![]() [decimal approximation]
[decimal approximation]
d. An angle of 3.89 radians will have its terminal side in what quadrant?
Solution: (one way to do this) Convert to degrees:
![]()
An angle of 222.9 degrees is in quadrant III, since 222.9 is between 180 and 270.
Special Triangles
You should know the following 30-60-90 right triangle and
45-45-90 right triangle. Radian equivalents for the angles are given in the
diagram. Note: ‘sqrt’ means square root, for instance, sqrt(3) = ![]() .
.
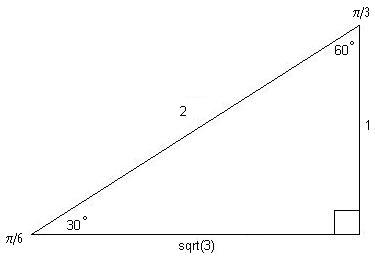
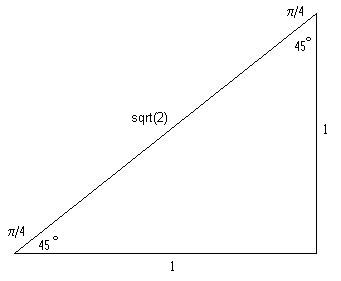
These triangles enable you figure out the trigonometric functions of the special angles 30, 45, and 60 degrees.
Reference Angles
If ![]() is an angle in standard
position, then
is an angle in standard
position, then ![]() ’s reference angle
’s reference angle ![]() is the
positive acute angle that the terminal side of
is the
positive acute angle that the terminal side of ![]() makes with the horizontal
axis.
makes with the horizontal
axis.
Here are the formulas (in terms of degrees – but you should
know them also in terms of radians) for calculating the reference angle in each
quadrant, given the angle ![]() .
.
Quadrant I: ![]()
Quadrant II: ![]()
Quadrant III: ![]()
Quadrant IV: ![]()
The above formulas are used to find a reference angle when
the angle itself is known. Very often it is the case, however, that the
reference angle ![]() is known and we need to find
the angle
is known and we need to find
the angle ![]() . Thus we need to use these
formulas in the following alternate forms:
. Thus we need to use these
formulas in the following alternate forms:
Quadrant I: ![]()
Quadrant II: ![]()
Quadrant III: ![]()
Quadrant IV: ![]()
Using reference angles
The usefulness of reference angles derives primarily from
the following fundamental fact: The trigonometric functions of an angle ![]() and its
reference angle
and its
reference angle ![]() are the same except possibly
for sign. The sign is determined according to quadrant, by using the sign
rules (the ASTC chart).
are the same except possibly
for sign. The sign is determined according to quadrant, by using the sign
rules (the ASTC chart).
Example. Evaluate ![]() [no calculator]
[no calculator]
Solution: step 1: find the reference angle: ![]() =
=![]() [note:
we’re in Quadrant IV]. Step 2: Use a special triangle to determine the
trigonometric function of the reference angle:
[note:
we’re in Quadrant IV]. Step 2: Use a special triangle to determine the
trigonometric function of the reference angle: ![]() , because csc is hypotenuse
over opposite. Step 3: we know now that our answer is either
, because csc is hypotenuse
over opposite. Step 3: we know now that our answer is either ![]() or
or ![]() . To
decide which, we use the sign rules (ASTC). Our angle,
. To
decide which, we use the sign rules (ASTC). Our angle, ![]() , is in quadrant
IV; the csc function is negative in quadrant IV and so our answer is
, is in quadrant
IV; the csc function is negative in quadrant IV and so our answer is ![]() .
.
Reference angles are also used to find angles when given the value of a trigonometric function, as in the next two examples.
Example. Given ![]() , find
, find ![]() with
with ![]() .
.
Note: in the specified interval, from 0 to 360 degrees, most questions of the sort will have two answers. (The only exceptions: some of the “boundary angles,” 0, 90, 180, and 270 degrees, but Homework 1 does not involve these).
Solution. Step 1: Use a special triangle to find the
positive acute angle with the given trigonometric function value, this will be
the reference angle. In this case, we see that ![]() and so
and so ![]() . Step 2: Decide
in what two quadrants there are answers. In this case, there is a Quadrant I answer,
say
. Step 2: Decide
in what two quadrants there are answers. In this case, there is a Quadrant I answer,
say ![]() ,
and a Quadrant II answer, say
,
and a Quadrant II answer, say ![]() , because these are the 2
quadrants where sin is positive (ASTC) and our given value (
, because these are the 2
quadrants where sin is positive (ASTC) and our given value (![]() ) is positive. For
each quadrant, use the appropriate formula to find the answer:
) is positive. For
each quadrant, use the appropriate formula to find the answer: ![]() and
and ![]() .
.
Example. Given ![]() , find
, find ![]() with
with ![]() .
.
Note: this time we are to use radians (because these are the units used to specify the interval); some students like to work this type of problem in terms of degrees and then convert the answers to radians in the end. That’s fine, but for practice working with radians, we’ll work this one entirely in radians.
Solution: Use a special triangle to determine the reference
angle (ignore the negative sign in this step). In this case, we see that ![]() , because
cot is adjacent over opposite, and so
, because
cot is adjacent over opposite, and so ![]() . Step 2: We have answers,
say
. Step 2: We have answers,
say ![]() and
and
![]() ,
in Quadrants II and IV, resp., because these are the two quadrants where cot is
negative. Step 3:
,
in Quadrants II and IV, resp., because these are the two quadrants where cot is
negative. Step 3: ![]() and
and ![]() .
.